- These trigonometric identities will help you understand how equations are equal and you will apply your understanding of these trigonometric identities in questions asking for you to use equivalent trigonometric expressions.
- The identities mostly used in this section are Co function identities for angles in the 1st and 2nd Quadrant.
- This means that you will use a specific trigonometric identity for the angle found in either the 1st or 2nd quadrant.
1st. Quadrant:
1. sin30º= cos60º, both approx. = 0.5000
2. sin50º= cos40º, both approx. = 0.7660
2nd. Quadrant:
1. -sin20º=cos110º, both approx. = -0.3420
2. sin100º=cos10º, both approx. = -0.1736
Key: degrees is substituted for the x value
We will come up with the following identities:
1st Quadrant:
1. sinx = cos((π/2)-x)
2. cosx = sin((π/2)-x)
2nd Quadrant:
1. sinx= cos(x+(π/2))
2. -cosx= sin(x+(π/2))
1. sin30º= cos60º, both approx. = 0.5000
2. sin50º= cos40º, both approx. = 0.7660
2nd. Quadrant:
1. -sin20º=cos110º, both approx. = -0.3420
2. sin100º=cos10º, both approx. = -0.1736
Key: degrees is substituted for the x value
We will come up with the following identities:
1st Quadrant:
1. sinx = cos((π/2)-x)
2. cosx = sin((π/2)-x)
2nd Quadrant:
1. sinx= cos(x+(π/2))
2. -cosx= sin(x+(π/2))
3rd Quadrant:
1. -sinx=cos(x+π)
2. -cosx=sin(x+π)
4rd Quadrant:
1. -sinx=cos(2π-x)
2. cosx=sin(2π-x)
Pythagorean Identities
For angle θ at which the functions are defined:
(1) cos2θ + sin2θ = 1
(2) 1 + tan2θ = sec2θ
(3) 1 + cot2θ = csc2θ
(2) 1 + tan2θ = sec2θ
(3) 1 + cot2θ = csc2θ
Dividing both sides of the first equation by cos2θ results in the second equation. Similarly, dividing both sides of the first equation by sin2θ results in the third equation.

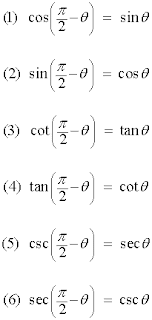
Really Help me to fight the term
ReplyDeletethanks bro …