4.1 Radian Measure

Figure 1. The curve boundary of length L is an arc

4.1 Radian measure

An arc is a segment of the circumference of a circle. Actually, the circumference itself can be considered an arc length

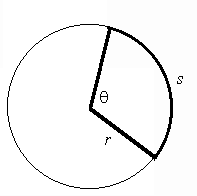
Figure 2.

The length, s, of an arc of a circle radius r subtended by θ (in radians) is given by:

s = rθ

If r is in meters, s will also be in meters. Likewise, if r is in cm, s will also be in cm.

Radian is the ratio between the length of an arc and its radius. 

Figure 3.  An angle of 1 radian results in an arc
with a length equal to the radius of the circle. 

The radian measure of an angle drawn in standard position in the plane is equal to the length of arc on the unit circle subtended by that angle. 

Converting Degrees to Radians

Because the circumference of a circle is given by C = 2πr and one revolution of a circle is 360°, it follows that:

2π radians = 360°.

This gives us the important result:

π radians = 180°

From this we can convert:

radians → degrees and

degrees → radians.

A full angle is therefore  radians, so there are  per  radians, equal to  or 57./radian. Similarly, a right angle is radians and a straight angle is  radians.